魔方陣のとても簡単な作り方~コツが分かれば小学生でも作れます

「魔方陣」(まほうじん)というものがあります。
一番小さいなものはタテヨコ3マスずつの方形で、マスのひとつひとつに1から9までの数字を各々はめ込み、縦・横・斜めの合計を同じにするというものです。3×3の魔方陣の場合、各列の合計が15になります。
子どもの遊びですが、タテヨコのマスの数を5にしたり9にしたりと、どんどん増やしていけばけっこう難しい問題になります。数学的にはややこしい計算をして作り上げるもののようです。
どうやったら作れるのかはウィキにも解説がありますが、ややこしくて分かりにくい方法です。私は、小学生のころに算数の得意な友達とふたりで簡単な作り方を考えつきました。
もちろん、世界で初めて見つけたハズはありませんが、あまり知られていないようなので、披露します。
スポンサーリンク
魔方陣とは?
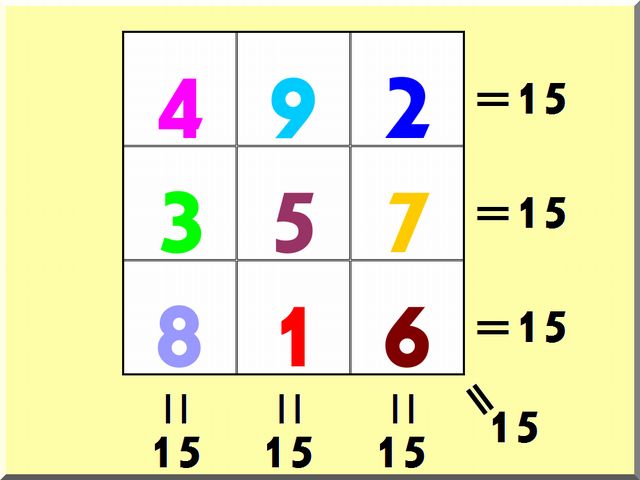
正方形のマス(方陣)の中に1から順にマスの数だけの数字を1つずついれていき、縦・横・斜めの合計が全て同じ値になるように、数字を配置したものです。3×3の魔方陣の場合、各列の合計は「15」になります。
どんなものも、1から最後の数までの合計を、縦(もしくは横)のマス数で割ったものが、各列の合計と一致します。例えば、3×3の場合、1から9までの数字が入りますが、1~9までをすべて足した合計45を3で割ると15。
これが魔方陣の縦横の合計に一致します。5×5(縦横全部で25マス)のものであれば、縦・横・斜めは、1から25までの合計325を5で割った65になるはずです。
尚、奇数×奇数のものと、偶数×偶数のものがありますが、私たちが考え出したものは奇数×奇数に限って使える方法です。
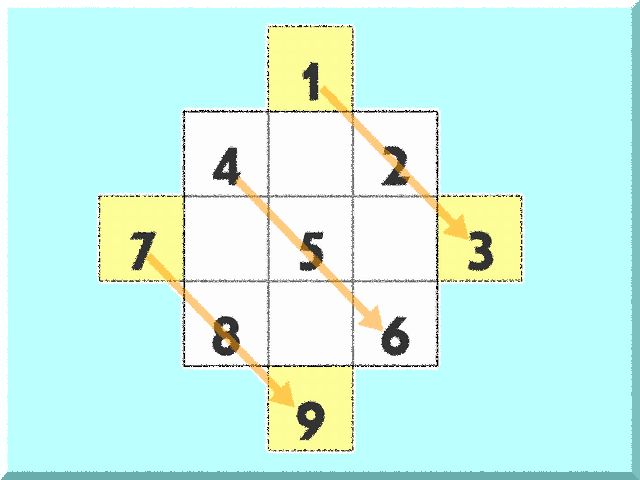
作り方は、まず外側にマスを追加して順に斜めに数字を入れていきます
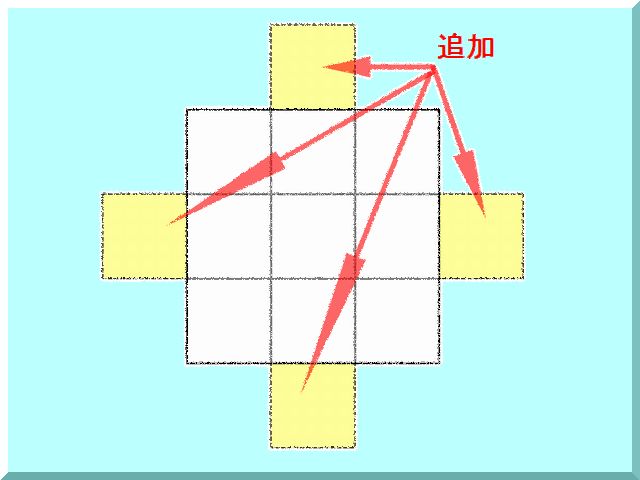
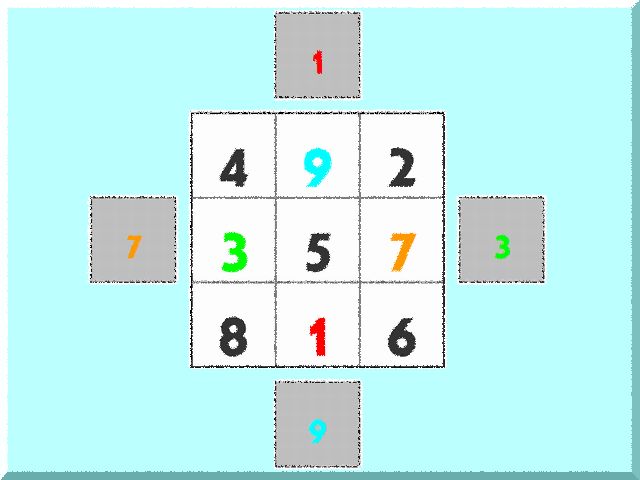
3×3方陣の各列の外側に、真ん中に一つずつマスを追加します。そして、頂点のマスから順に斜めに、1、2、3……9と数字を入れていきます。
はみ出した数字を対面の空いているマスにはめ込みます
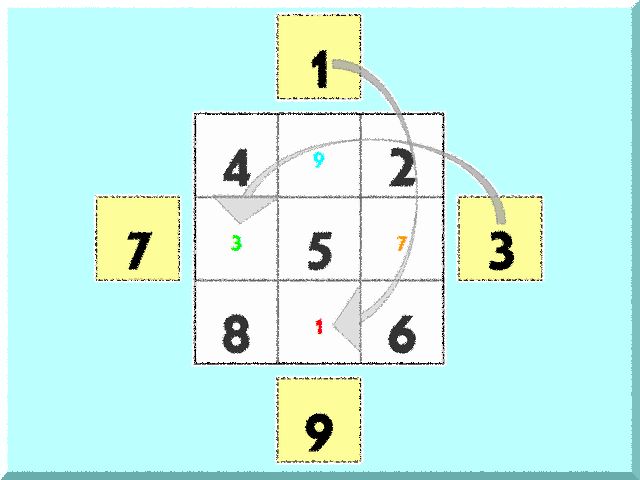
上の頂点にある「1」を一番下の空いているマスに、右側の頂点にある「3」を一番左の空いているマスに、左の「7」を右の空いているマスに、下の「9」を上の空いているマスにそれぞれ、移動させます。これだけ!です。
この作業をするだけで、正確な魔方陣ができあがりました! 縦・横・斜めの合計を計算してみてください。いずれも15になっています。
5×5の時はどうするのか?
3×3の時は、真ん中にひとつマスを追加するだけですが、5×5、7×7、9×9と数が増えていくと少しややこしくなります。
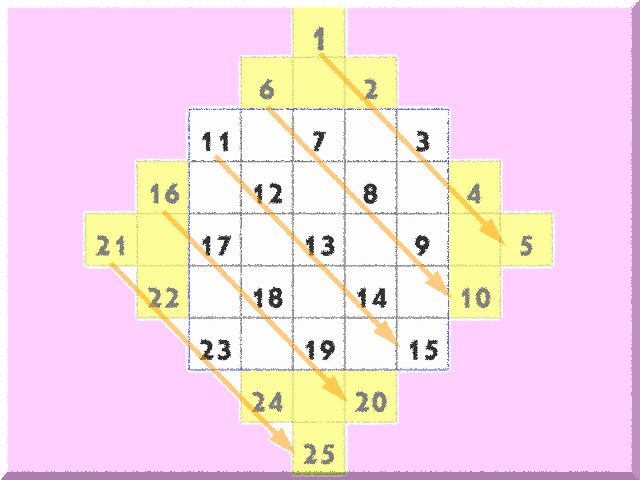
1列5つのマスのうち、真ん中の3つの外側にピラミッドを作るようにマスを積み上げます。(すぐ外側に3列マスを増やしたその上の中央にさらに1マス作ります)
例えば、一番上の列なら、5つのマスの上の中央に3マス追加し、その上に1マス加えます。
スポンサーリンク
その上で、3×3のときと同じ要領で、頂点をスタートに1から順に数字を斜めに入れていきます。「5」まで入れたら、今度は「6」を「1」の斜め左下のマスから始めてください。
「11」から「15」は方陣の対角線に入ることになり、「16」は方陣の外からスタートすることになります。「21」は左端の頂点からスタートし、「25」は最下段の頂点でエンドです。
「山」を切り取って、対面にはめ込みます
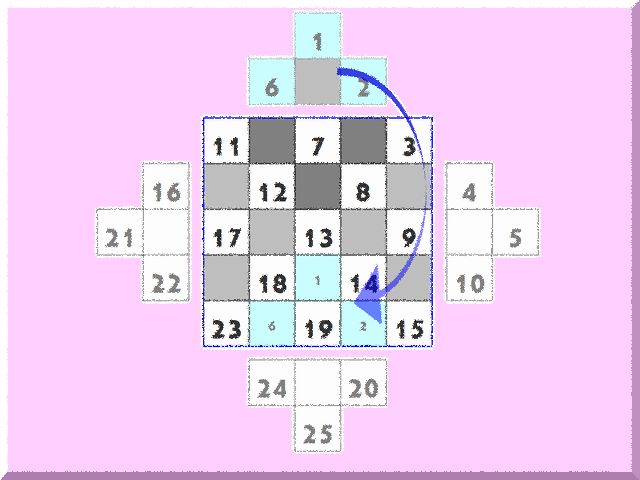
25まで入れ終えたら、今度ははみ出している「山」の部分を移動させます。3×3のときと同様に、上の「山」を一番下の空白のマスに、右の山を左端の空白のマスに、下の山を上の空白に、左の山を右の空白にそれぞれ、はめ込んでみましょう。
これで、5×5の魔法陣の完成です。縦・横・斜めの合計を計算してみてください。それぞれ「65」になるはずです。
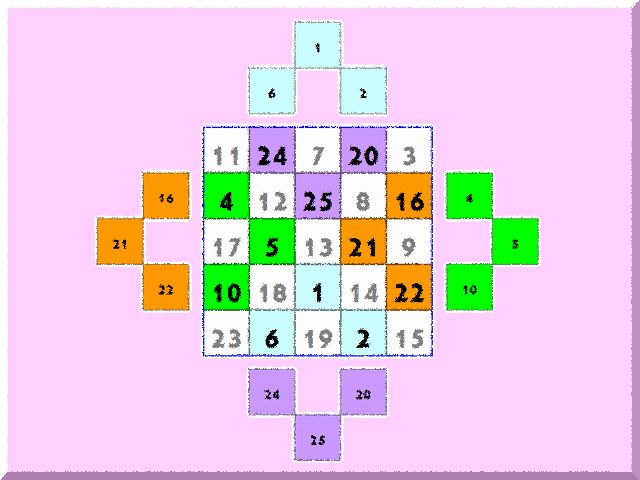
7×7、9×9も同じようにできます
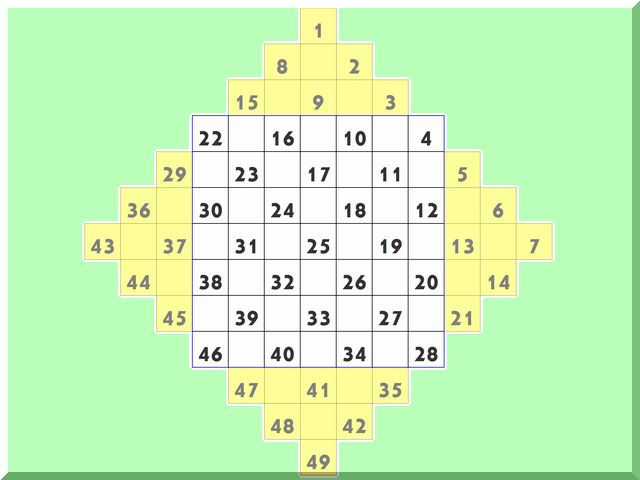
これから先は、数が増えても同じです。7×7の場合は、追加する「山」の底辺が5マスになるだけです。これまでと同様に、頂点から順に数字を入れていき、端まで行き着いたら左上に戻って、また斜めに入れていきます。すべての数字を入れ終えたら、山を切り取って反対側に移動させるだけ。
魔方陣の特徴は?
こうして作ってみると、一定の規則というかパターンがあることがわかります。まず、中央値(真ん中の数:7×7の場合は「25」)は、必ず方陣の中心にくるということ。その中央値を囲んで、対角線上には連続する数字が並ぶこと(7×7の場合、22,23,24,25,26,27,28が対角線上に並ぶ)。
それと交差する対角線上には、中央値の等差数列が並ぶこと(7×7の場合、4,11,18,25,32,39,46:等差は7)。最小値である1と最大値は必ず中央値の上下に並ぶこと、などです。規則的に数字をはめ込んでいるので、結果に何がしかの規則が生まれるのは当然といえば当然なのですが。
いくつに増えてもできるのか
実は、どうしてこれで魔方陣ができるのか、私には分かりません。タダの小学生が遊んでいるうちに、偶然うまく行く方法を見つけただけなので、理論的な裏付けはありません。そのため、どんなに数が増えてもこの方法でうまくいくのかどうかはわからないのです。
小学生時代には、25×25までの方陣について実際に作って試してみたところ、全てうまくいきました。3×3から25×25までうまくいくのですから、この先もうまくいくはずだろうと、推論します。
当時は、手計算でしたのでこの程度までしかチャレンジできませんでしたが、今ならエクセルを使えばすぐにタテヨコの計算ができるので、検証は簡単です。どなたか興味のある人は、99×99などを試してみてください。
もっとも、簡単につくれる方法が分かってしまうと、知恵を絞って作り上げる楽しみはなくなってしまうのですけれども。
by 水の
スポンサーリンク